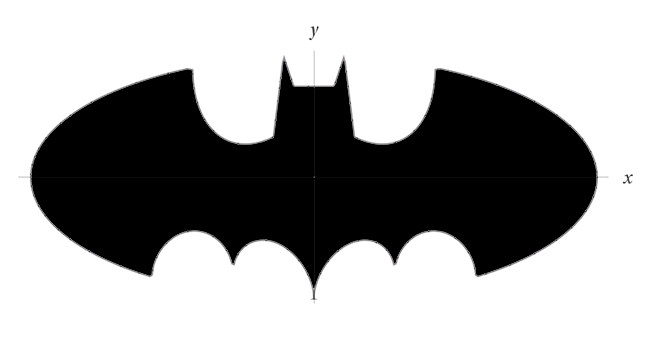
Μα το φάντασμα του Leibniz, ο Μπάτμαν!!! Τον τελευταίο καιρό κυκλοφορεί μια συνάρτηση, η οποία ισχυρίζονται πως όταν την σχεδιάσεις σου δίνει το γνωστό λογότυπο του Μπάτμαν.
Καταρχάς, να πούμε αυτή η συνάρτηση αυτή δεν προκύπτει από την επίλυση κάποιας (έστω και λίγο) χρήσιμης σχέσης, αλλά σχεδιάστηκε από κάποιον με στόχο η γραφική της παράσταση να έχει τη συγκεκριμένη μορφή.
Πάμε λίγο στα πιο τεχνικά! Πρόκειται για μια εξίσωση της μορφής ![]() , η οποία επιλύεται στο σύνολο των μιγαδικών
, η οποία επιλύεται στο σύνολο των μιγαδικών ![]() και σχεδιάζεται για πραγματικές τιμές των
και σχεδιάζεται για πραγματικές τιμές των ![]() . Η συνάρτηση
. Η συνάρτηση ![]() προκύπτει από τον πολλαπλασιασμό
προκύπτει από τον πολλαπλασιασμό ![]() διαφορετικών συνιστωσών.
διαφορετικών συνιστωσών.
Καθεμία από τις συνιστώσες είναι μια στοιχειώδης καμπύλη – ευθεία κατάλληλα τροποιημένη με κάποιο “τρικ” έτσι ώστε να αποκοπεί ένα μέρος της γραφικής παράστασης. Το “τρικ” αυτό βασίζεται στην χρήση ριζών και απολύτων:
![]()
Έτσι διασφαλίζουμε πως στην γραφική παράσταση θα είναι ορατό το τμήμα με ![]() .
.
Συνιστώσα 1η: Άκρες φτερών
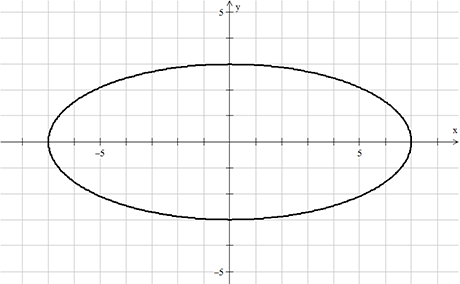
Η πρώτη ύλη μας είναι η έλλειψη ![]() .
.
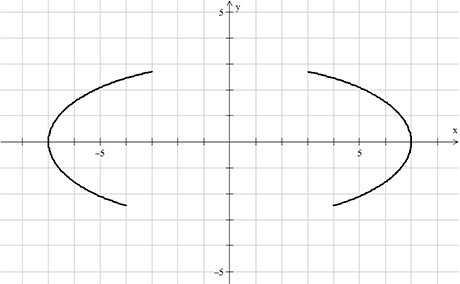
Για το λογότυπο, όμως, μας ενδιαφέρουν τα τμήματα όπου ![]() και
και ![]() .
.
Χρησιμοποιώντας το παραπάνω “τρικ”, δημιουργούμε την ζητούμενη καμπύλη με την εξίσωση 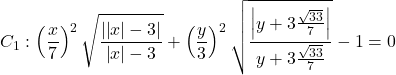 .
.
Συνιστώσα 2η: Κάτω μέρος φτερών
Η 2η συνιστώσα αποτελείται από δύο ξεχωριστές καμπύλες. Η μία καμπύλη είναι μια παραβολή στο θετικό ημιάξονα ![]() που έχει ανακλαστεί πάνω στον άξονα
που έχει ανακλαστεί πάνω στον άξονα ![]() .
.
![]()
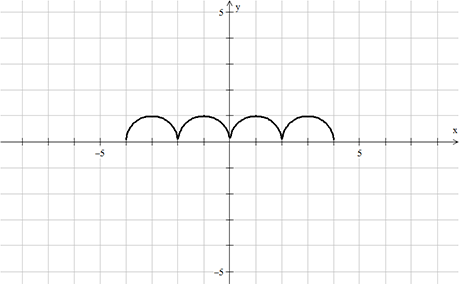
Η άλλη καμπύλη είναι τα 4 πάνω ημισφαίρια κύκλων.
![]()
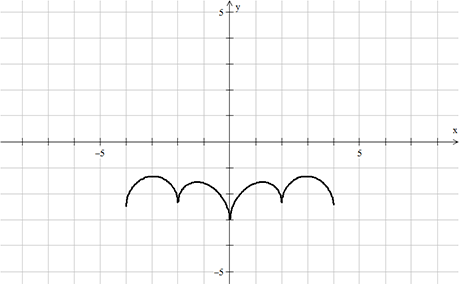
Κατόπιν προσθέτουμε τις ![]() και
και ![]() και προκύπτει η 2η συνιστώσα.
και προκύπτει η 2η συνιστώσα.
![]()
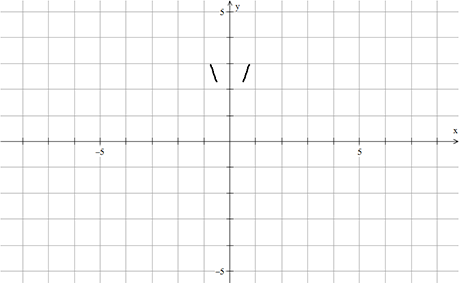
Συνιστώσα 3η και 4η: Αυτιά
Τα αυτιά δημιουργούνται από δύο καμπύλες. Η πρώτη σχηματίζει τις 2 εξωτερικές γραμμές και η δεύτερη τις 2 εσωτερικές γραμμές.
Η 3η είναι το ζεύγος των ευθειών ![]() με τιμές στην περιοχή
με τιμές στην περιοχή ![]() .
.
![Rendered by QuickLaTeX.com \[ \displaystyle C_{3} : 9\sqrt{\frac{\left( \left| \left( 1-\left| x \right| \right)\left( \left| x \right|-0.75 \right) \right| \right)}{\left( 1-\left| x \right| \right)\left( \left| x \right|-0.75 \right)}}\; -\; 8\left| x \right|\; -\; y\; =\; 0 \]](https://bakouros.gr/wp-content/ql-cache/quicklatex.com-48cda985df4772f1793e40c6a3bc02e4_l3.png)
Παρόμοια, η 4η είναι το ζεύγος των ευθειών ![]() με τιμές στην περιοχή
με τιμές στην περιοχή ![]() .
.
![Rendered by QuickLaTeX.com \[ \displaystyle C_{4} : 3\left| x \right|\; +\; 0.75\sqrt{\left( \frac{\left| \left(0.75-\left| x \right| \right)\left( \left| x \right|-0.5 \right) \right|}{\left(0 .75-\left| x \right| \right)\left( \left| x \right|-0.5 \right)} \right)}\; -\; y\; =\; 0 \]](https://bakouros.gr/wp-content/ql-cache/quicklatex.com-a93dbaf47cc90a764cdb846f90f65a38_l3.png)
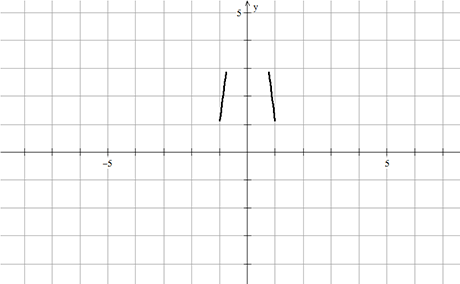
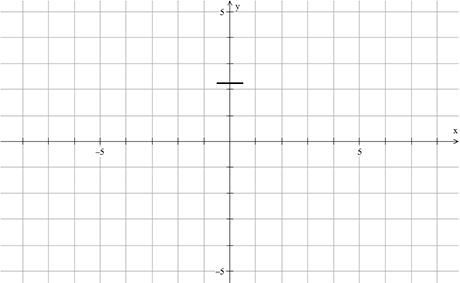
Συνιστώσα 5η: Κεφάλι
Το κεφάλι δημιουργείται από την γραμμή ![]() με τιμές στην περιοχή
με τιμές στην περιοχή ![]() .
.
![Rendered by QuickLaTeX.com \[ \displaystyle C_{5} : 2.25\sqrt{\frac{\left| \left( 0.5-x \right)\left( x+0.5 \right) \right|}{\left( 0.5-x \right)\left( x+0.5 \right)}}\; -\; y\; =\; 0 \]](https://bakouros.gr/wp-content/ql-cache/quicklatex.com-f41d6a9d468d6dd16b511bcb49cb97d0_l3.png)
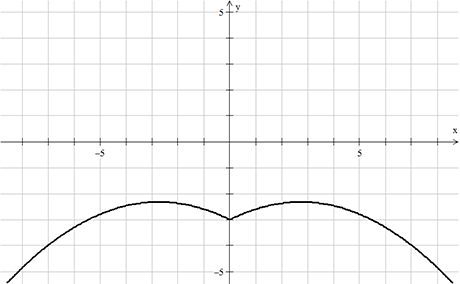
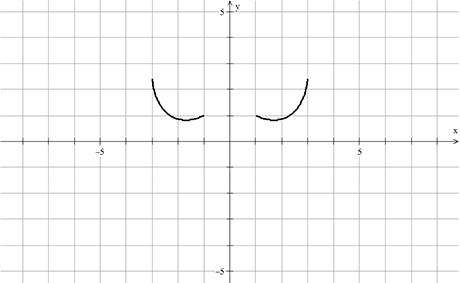
Συνιστώσα 6η: Πάνω μέρος φτερών
Η τελευταία συνιστώσα σχηματίζει το πάνω μέρος των φτερών και δίνεται από την εξίσωση:
![Rendered by QuickLaTeX.com \[ C_{6} : \begin{matrix} \frac{6\sqrt{10}}{7}\; +\; \left( 1.5\; -\; .5\left| x \right| \right)\sqrt{\frac{\left| \left| x \right|-1 \right|}{\left| x \right|-1}}\; -\; \\ \frac{\left( 6\sqrt{10} \right)}{14}\sqrt{4-\left( \left| x \right|-1 \right)^{2}}\; -\; y\; =\; 0 \end{matrix} \]](https://bakouros.gr/wp-content/ql-cache/quicklatex.com-dae95cf7cb6202aa55a7bacb3e6a8bfc_l3.png)
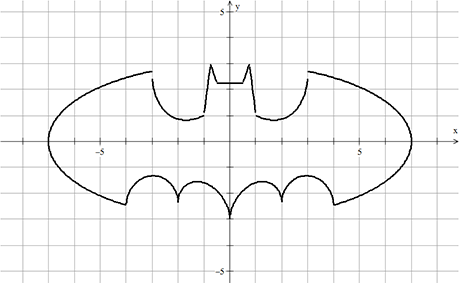
Και τώρα ήρθε η μεγάλη ώρα!! Η τελική εξίσωση προκύπτει ως ![]() .
.
Και να το πολυπόθητο αποτέλεσμα! Σίγουρα ένα εγχείρημα αντάξιο του μεγαλείου του Μπάτμαν!!
Υ.Γ. Καλή Χρονιά και Καλή μας αρχή!!!











No comments